Texas Holdem Hand Trips
Evolution’s Ultimate Texas Hold’em Poker is streamed out of Latvia, just like their Trips Bonus Bet game. The game is mobile-friendly, so, it can be played on all modern iOS and Android-powered smartphone and tablet devices. The basic game doesn’t contain side-bets, so you’re going to want to play the Triple Bonus Bet version for those. Unlike traditional Texas Hold ‘Em variations, however, these two wagers must be equal. There is also an optional Trips side bet which pays regardless of whether your hand wins or loses. Read on to learn more about Ultimate Texas Hold ‘Em payouts, rules and how to play. Ultimate Texas Hold ‘Em Articles.
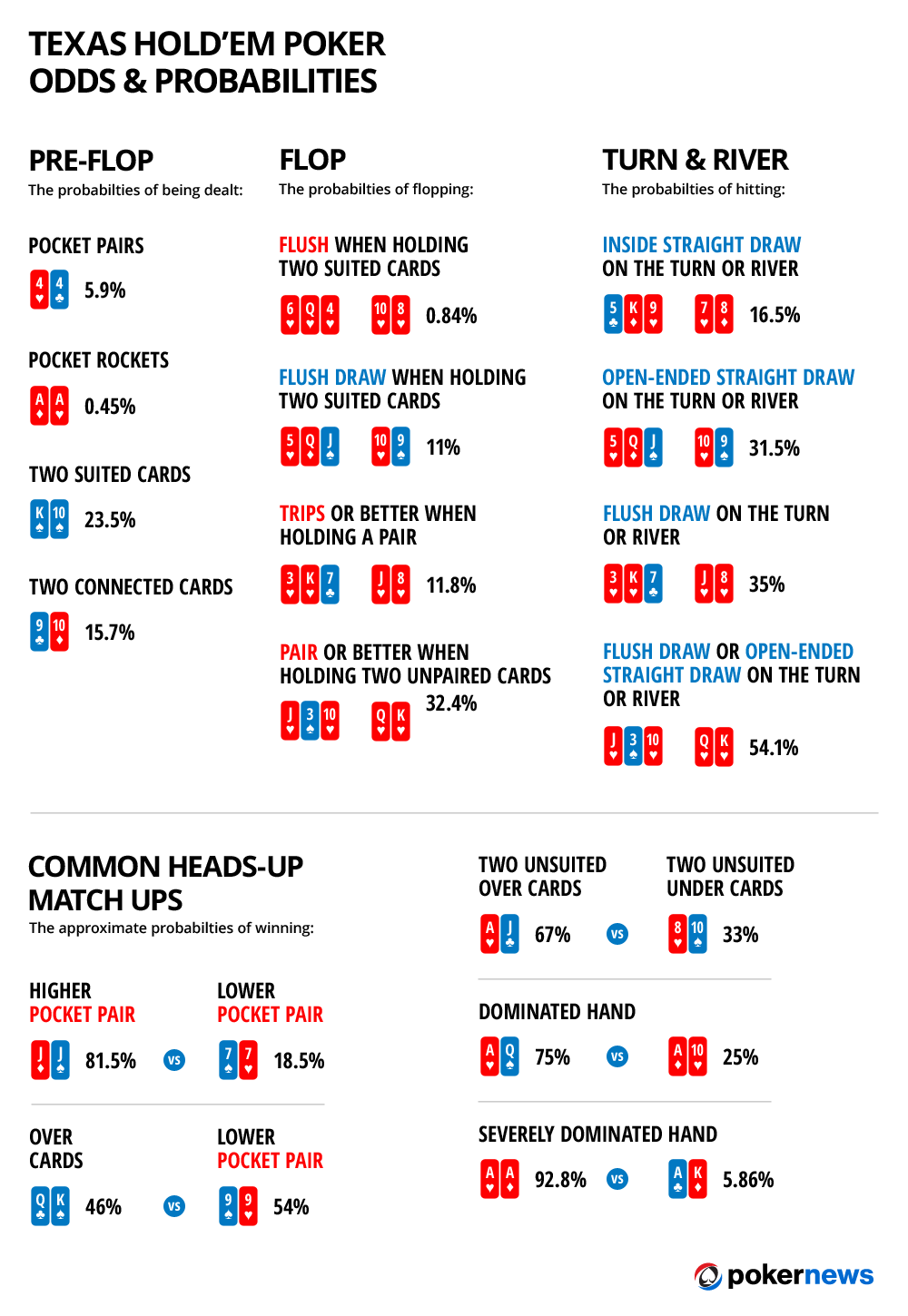
Playing poker is about playing the odds. The following list gives the odds for outcomes in Texas Hold’em hands. When you realize how heavily the odds are stacked against you, you may want to rethink going all-in before the flop with two suited cards. Use the odds to your advantage:
1 percent (1-in-100): Percentage of time that no player holds an Ace or a King at a table in a 10-handed game
1 percent (1-in-100): Percentage of time that if you hold two suited cards, you’ll flop a flush
6 percent (about 1-in-20): Percentage of time that five community cards will give pocket suited cards a flush
6 percent (about 1-in-20): Percentage of time that you’ll be dealt a pocket pair
8 percent (about 1-in-12): Percentage of time that you’ll hit at least trips after having a pair on the flop
12 percent (about 1-in-8): Percentage of time that you’ll flop trips if holding a pocket pair
12 percent (about 1-in-8): Percentage of time that two more cards will flop in the same suit as a suited pocket pair
19 percent (about 1-in-5): Percentage of time that the five community cards will at least trip your pocket pair
32 percent (about 1-in-3): Percentage of time that you’ll pair one of your cards on the flop (with no pocket pair)
33 percent (about 1-in-3): Percentage of time that you’ll make a full house or better after having trips on the flop
35 percent (about 1-in-3): Percentage of time that you’ll make a flush on the turn or river if you have four cards to a flush after the flop
How much bigger is the house edge for trips on Ultimate Texas Holdem if trips is ONLY paid on hands where the player wins?
Trips Payout Scale:
50
40
30
8
7
4
3
Administrator
I've been to casinos where trips is paid regardless if the player wins the hand. I've also been to casinos where trips is ONLY paid if the player wins the hand.
How much bigger is the house edge for trips on Ultimate Texas Holdem if trips is ONLY paid on hands where the player wins?
Trips Payout Scale:
50
40
30
8
7
4
3
Fwiw. Trips is designed to be an independent event. The distributor (Scientific Gaming Inc) does not want casinos to offer the game in a fashion that requires the player to bet the play if they don't want to. Last I heard, when SCI hears of those procedures, they go to the casino and insist the game is offered in accordance with the lease. So you might consider informing them of any casino that's currently doing this.
It's come up before. If I recall correctly, it adds less than 1% to the game HE, because it doesn't come up that often. Maybe someone has an actual number?
It would take a result on the board like trips or quads, perhaps a flush with a deuce on the board in limited cases (like somehow you know nobody else on your full table has the board flush suit in hand). Otherwise you'd be playing for the push and win, and be in anyway.
OK, I read your post again. I think I misunderstood what you asked, because what I described is a pet peeve of mine.
There are states/jurisdictions where the player MUST win the Trips bet to get paid. The paytable for those are usually better than the one you posted because of that. I think you probably quoted one where you don't have to win to get paid.
The places I've seen that beat the dealer rule are in Florida (non-NA card rooms - the Seminoles pay it properly ), some parts of CA, and several Indian casinos. I just refuse to play in their casinos.
In this casino a push between the player and dealer will result in a trips bet push as well.
If nobody else gets to this, I’ll be on it later tonight or tomorrow for you. It’s pretty easy, just time consuming.
Fwiw. Trips is designed to be an independent event. The distributor (Scientific Gaming Inc) does not want casinos to offer the game in a fashion that requires the player to bet the play if they don't want to. Last I heard, when SCI hears of those procedures, they go to the casino and insist the game is offered in accordance with the lease. So you might consider informing them of any casino that's currently doing this.
It's come up before. If I recall correctly, it adds less than 1% to the game HE, because it doesn't come up that often. Maybe someone has an actual number?
It would take a result on the board like trips or quads, perhaps a flush with a deuce on the board in limited cases (like somehow you know nobody else on your full table has the board flush suit in hand). Otherwise you'd be playing for the push and win, and be in anyway.
OK, I read your post again. I think I misunderstood what you asked, because what I described is a pet peeve of mine.
There are states/jurisdictions where the player MUST win the Trips bet to get paid. The paytable for those are usually better than the one you posted because of that. I think you probably quoted one where you don't have to win to get paid.
The places I've seen that beat the dealer rule are in Florida (non-NA card rooms - the Seminoles pay it properly ), some parts of CA, and several Indian casinos. I just refuse to play in their casinos.
You are right. I posted the wrong the trips payout scale. The correct trips payout scale for this casino is:
50
40
30
10
8
6
3
You have to beat the dealer to win the trips bet. A push with the dealer result in a trips bet push.
If I calculated it correctly, this results in +0.139601% return for the trips bet which makes it appear attractive at first glance but that doesn't take into account that you don't get paid on trips bet unless you beat the dealer.
Edit: Thanks for your time and replies.WoT
If nobody else gets to this, I’ll be on it later tonight or tomorrow for you. It’s pretty easy, just time consuming.
Thanks, I appreciate your time and replies. I've included the correct trips payout scale in an earlier post. I posted the wrong payout scale in the original post.beachbumbabs
Administrator
You are right. I posted the wrong the trips payout scale. The correct trips payout scale for this casino is:
50
40
30
10
8
6
3
You have to beat the dealer to win the trips bet. A push with the dealer result in a trips bet push.
If I calculated it correctly, this results in +0.139601% return for the trips bet which makes it appear attractive at first glance but that doesn't take into account that you don't get paid on trips bet unless you beat the dealer.
Edit: Thanks for your time and replies.
Yeah, if you're coming up with .14%, there's something wrong there. It's more like 9-10%, where the regular Trips paytables are 5-7%
Yeah, if you're coming up with .14%, there's something wrong there. It's more like 9-10%, where the regular Trips paytables are 5-7%
My mistake again. I meant 14%.Mission146
You are right. I posted the wrong the trips payout scale. The correct trips payout scale for this casino is:
50
40
30
10
8
6
3
You have to beat the dealer to win the trips bet. A push with the dealer result in a trips bet push.
If I calculated it correctly, this results in +0.139601% return for the trips bet which makes it appear attractive at first glance but that doesn't take into account that you don't get paid on trips bet unless you beat the dealer.
Edit: Thanks for your time and replies.
Okay, so the first thing that we want to do is calculate the overall return for the paytable listed above as if losing the main bet did not lose the Trips bet. We can get our probabilities from the WoO UTH page:
https://wizardofodds.com/games/ultimate-texas-hold-em/
(50 * 0.000032) + (40 * 0.000279) + (30 * 0.001681) + (10 * 0.025961) + (8 * 0.030255) + (6 * 0.046194) + (3 * 0.048299) - (.8473) = 0.139601
This results in an expected profit of .139601 units, which is a 13.9601% player advantage.
Now, we have an even easier job than I thought thanks to the Bad Beat side bet in Liechtenstein, which is listed on the WoO UTH page:
https://wizardofodds.com/games/ultimate-texas-hold-em/
This bet pays varying amounts if either player or dealer lose with a 3OaK, or better. All we need to do to get the overall percentage we need to subtract from above is to subtract half of the bad beat probability from each hand from the overall probability. (Player and Dealer each do it half the time) The table for this also conveniently includes the Push rate for us!
Straight Flush: 0.000004/2 = .000002
4OaK: 0.000169/2 = .0000845
Full House: 0.003033/2 = .0015165
Flush: 0.006987/2 = 0.0034935
Straight: 0.006569/2 = .0032845
3OaK = 0.023028/2 = .011514
Okay, so each of these individual probabilities need to be subtracted from the wins on the formula above. The cumulative probability also must be added to the loss rate, so let's go ahead and get that:
.000002 + .0000845 + .0015165 + .0034935 + .0032845 + .011514 = 0.019895
Now, we have to adjust the formula above:
(50 * 0.000032) + (40 * (0.000279-.000002)) + (30 * (0.001681-.0000845)) + (10 * (0.025961-.0015165)) + (8 * (0.030255-.0034935)) + (6 * (0.046194-.0032845)) + (3 * (0.048299-.011514)) - (.8473 +.019895) = 0.019729
Okay, that returns an expected return of 1.9729 cents per dollar bet, but this does not include pushes.
We're going to have to get a little creative to approximate a Push rate here. The first thing that we know is that the following hands can only be pushed with all five on the board:
Royal*
Straight Flush*
4OaK
Full House
Flush*
Straight
3OaK
Therefore, the probability of pushing those hands is instantly the same as the five card probabilities for each hand:
0.00000154+.0000139+.001965= 0.00198044
Thus, we subtract those from the win rates for each respective hand:
(50 * (0.000032-.00000154)) + (40 * (0.000279-.000002-.0000139)) + (30 * (0.001681-.0000845)) + (10 * (0.025961-.0015165)) + (8 * (0.030255-.0034935-.001965)) + (6 * (0.046194-.0032845)) + (3 * (0.048299-.011514)) - (.8473 +.019895) = 0.003376
That knocks us down to an expected win of .003376 or a player advantage of 0.3376%.
This does not account for pushing with a 4OaK, Full House, Straight or 3OaK.
What we do know is that a Full House on the board would either have to push, or would be a win for either the player or the dealer. The wins for the dealer FH beating the player FH have already been accounted for. A hand such as AA999 with either the player (or dealer) having an Ace, but not the other, would be a win for the dealer or player. If both dealer and player had an Ace, then this hand would again be a push. Player or dealer winning with both having FH have already been accounted for.
For the purposes of approximation, let's just assume that any FH on the board is a push.
(50 * (0.000032-.00000154)) + (40 * (0.000279-.000002-.0000139)) + (30 * (0.001681-.0000845)) + (10 * (0.025961-.0015165-.001441)) + (8 * (0.030255-.0034935-.001965)) + (6 * (0.046194-.0032845)) + (3 * (0.048299-.011514)) - (.8473 +.019895) = -0.011034
By itself, that brings us to an expected loss of 1.1034 cents (very approximated) for each dollar bet. This represents, at a minimum, a 1.1034% house edge.
That leaves us with Push 3OaK's, Straights and 4OaK's, and all of that is, unfortunately, above my pay grade. I also can't see any easy way to find those figures.
For what it's worth, the majority of board straights will push and the probability of a board straight is .003925. Any Ace high board straight will push, so that probability is:
(20/52 * 16/51 * 12/50 * 8/49 * 4/48) - 0.00000154 = 0.00039246375 (The .00000154 subtracts royals)
Next, the probability of any other dealt straight is: .003925 - .00039246375 = 0.00353253625
The probability that neither dealer or player will have the next card to continue other straights is:
(43/47 * 42/46 * 41/45 * 40/44) = 0.69189583158
So (0.00353253625*.69189583158) + .00039246375 = 0.00283661085
Is the probability of an Ace high straight, or a straight in which both dealer and player cannot continue the straight.
(50 * (0.000032-.00000154)) + (40 * (0.000279-.000002-.0000139)) + (30 * (0.001681-.0000845)) + (10 * (0.025961-.0015165-.001441)) + (8 * (0.030255-.0034935-.001965)) + (6 * (0.046194-.0032845-0.00283661085)) + (3 * (0.048299-.011514)) - (.8473 +.019895) = -0.0280536651
That brings us to a House Edge of 2.80536651% which doesn't include:
A.) The fact that some three-to-a-straight and four-to-a-straights on the board will push with both having straights.
B.) The fact that some five card straights on the board will be continued by both player and dealer and will push.
C.) The fact that a few 4OaKs will push. All of which will be on the board.
D.) The fact that some 3OaKs will push.
E.) Assumes that any FH on the board will push, which isn't true, but is somewhat offset by the fact that we are not including Two Pairs on the board which both dealer and player turn into a Full House of the same rank.
All 4OaK must be on the board and roughly 1/13 would include an Ace kicker or be Aces with a King kicker.
.000240 * 1/13 = 0.00001846153
All other 4 Oaks are .000240-.00001846153= 0.00022153847
(50 * (0.000032-.00000154)) + (40 * (0.000279-.000002-.0000139)) + (30 * (0.001681-.0000845-.00001846153)) + (10 * (0.025961-.0015165-.001441)) + (8 * (0.030255-.0034935-.001965)) + (6 * (0.046194-.0032845-0.00283661085)) + (3 * (0.048299-.011514)) - (.8473 +.019895) = -0.028607511
Also, many 4OaKs will not have an Ace kicker, but neither player or dealer will be able to outkick the kicker.
Texas Holdem Premium Hands
King Kicker, No Ace 0.00022153847 * (43/47 * 42/46 * 41/45 * 40/44) = 0.00015328154
Queen Kicker, NO AK 0.00022153847 * (39/47 * 38/46 * 37/45 * 36/44) = 0.00010215995
Jack Kicker, No QKA 0.00022153847 * (35/47 * 34/46 * 33/45 * 32/44) = 0.0000650338
10 Kicker, No J-A 0.00022153847 * (31/47 * 30/46 * 29/45 * 25/44) = 0.00003489387
9 Kicker, No 10-A 0.00022153847 * (27/47 * 26/46 * 25/45 * 24/44) = 0.00002179799
8 Kicker, No 9-A 0.00022153847 * (23/47 * 22/46 * 21/45 * 20/44) = 0.00001099836
7 Kicker, No 8-A 0.00022153847 * (19/47 * 18/46 * 17/45 * 16/44) = 0.00000481419
 6 Kicker, No 7-A 0.00022153847 * (15/47 * 14/46 * 13/45 * 12/44) = 0.00000169539
6 Kicker, No 7-A 0.00022153847 * (15/47 * 14/46 * 13/45 * 12/44) = 0.000001695395 Kicker, No 6-A 0.00022153847 * (11/47 * 10/46 * 9/45 * 8/44) = 0.00000040987691
4 Kicker, No 5-A 0.00022153847 * (7/47 * 6/46 * 5/45 * 4/44) = 0.0000000434717935
3 Kicker, All Deuces 0.00022153847 * (4/47 * 3/46 * 2/45 * 1/44) = 0.00000000124205124
That means an additional:
0.00000000124205124+0.0000000434717935+0.00000040987691+0.00000169539+0.00000481419+0.00001099836+0.00002179799+0.00003489387+0.0000650338+0.00010215995+0.00015328154 = 0.00039512968 of the 4OaK will tie by those means.
(50 * (0.000032-.00000154)) + (40 * (0.000279-.000002-.0000139)) + (30 * (0.001681-.0000845-.00001846153-.00039512968)) + (10 * (0.025961-.0015165-.001441)) + (8 * (0.030255-.0034935-.001965)) + (6 * (0.046194-.0032845-0.00283661085)) + (3 * (0.048299-.011514)) - (.8473 +.019895) = -0.0404614014
That brings us to a 4.04614014% House Edge not including:
A.) The fact that some three-to-a-straight and four-to-a-straights on the board will push with both having straights.
B.) The fact that some five card straights on the board will be continued by both player and dealer and will push.
C.) The fact that a few 4OaKs will push that we have not listed by way of dealer and player having the same kicker card in each of their hands.
D.) The fact that some 3OaKs will push.
E.) Assumes that any FH on the board will push, which isn't true, but is somewhat offset by the fact that we are not including Two Pairs on the board which both dealer and player turn into a Full House of the same rank.
In any case, we have conclusively determined that this is not a player advantage despite the paytable that appears liberal. A surprising number of these hands will either push or will be beaten by the dealer. In sum, (1-(0.919536+0.040674))/2 = .019895, or nearly 2% of all hands, will have the player with 3OaK or better getting beaten by the dealer.
I'm going to guess that, if we factor in the missing hands, the house edge is probably going to come out in the neighborhood of 5%. Why any casino would want to offer this weird side bet is beyond me. Part of what players seem to like about the Trips bet is that they profit (or at least get some money back) when they have a strong hand that is beaten by the dealer. They also get paid for pushes.
Getting into anything that requires actual simulation or programming is beyond my abilities, sorry about that. Honestly, I thought I saw something on Heads-Up Texas Hold 'Em somewhere that discussed the overall probabilities of pushing each given hand rank on the final hand (that would have made this much easier) but I was either mistaken or just can't seem to find it again.
